Regressão Linear na prática - usando o R
É possível prever a pontuação de um time de futebol usando indicadores financeiros do ano anterior?
Essa semana, um grande amigo Contador me pediu para olhar um trabalho que ele estava desenvolvendo.
Seu objetivo era avaliar se existe correlação entre indicadores financeiros dos clubes de futebol e as respectivas pontuações no campeonato brasileiro.
Falamos que duas variáveis são correlacionadas quando a variação no valor de uma das variáveis indica que também deve haver uma variação no valor da outra variável. Ou seja, elas não são independentes.
Por exemplo, suponha que precisamos estimar o preço de um apartamento em determinado bairro.
O tamanho do imóvel (m²) provavelmente será correlacionado ao seu preço. Nesse caso, eles terão uma correlação positiva, pois quanto maior o apartamento, maior o preço.
Porém, outra variável que pode influenciar é a idade do apartamento. Porém, nesse caso, será uma correlação negativa. Isso porque quanto maior a sua idade, menor tende a ser o seu valor.
Voltando ao nosso caso, calculei todas as correlações que ele me pediu.
Eram 8 variáveis financeiras. A variável que mais se relacionou a pontuação dos clubes foi a Liquidez Imediata, a correlação foi de -0,202.
O coeficiente de correlação varia entre -1 e 1. Os valores próximos de -1 indicam correlação negativa muito forte. Os valores próximos de 1 indicam correlação positiva muito forte.
Os valores próximos a 0 indicam que não existem correlação linear entre as variáveis.
Então, fiz duas propostas para o trabalho:
Podemos prever a pontuação de cada clube usando variáveis financeiras?
E se compararmos a pontuação do clube com os índices financeiros do último ano?
Na minha opinião, essa última faz sentido pela lógica de como todo o planejamento de um clube de futebol funciona. Muitas vezes o time é montado antes dos campeonatos, ou seja, no ano anterior.
Ou, caso um time receba muito dinheiro em um ano, os benefícios vão ser refletidos nos anos seguintes.
Regressão Linear na prática
A regressão linear é um modelo estatístico que utiliza informações já conhecidas para se construir um modelo de previsão.
Em nosso caso isso significa criar um modelo para prever a pontuação dos times de futebol a partir dos índices financeiros de cada clube.
Os índices financeiros são as nossas variáveis preditivas, enquanto a pontuação no ranking é a nossa variável resposta.
A regressão linear pode ser simples ou múltipla.
Será regressão linear simples caso você utilize o valor de uma variável para prever outra variável.
Em nosso caso, vamos usar mais de uma variável para prever a pontuação dos clubes, portanto será uma regressão linear múltipla.
Uma preocupação muito importante e muitas vezes negligenciada é a seguinte:
- Quando você for fazer previsões com o seu modelo, quais informações estarão disponíveis?
É muito importante prestar atenção nesse detalhe. Não podemos construir um modelo estatístico e, quando formos colocar em prática, perceber que as informações que precisaríamos não estão disponíveis.
Nesse exemplo, seria tentador prever a pontuação dos clubes usando as variáveis financeiras do mesmo ano.
Porém, se pensarmos na prática, as variáveis financeiras só estarão disponíveis depois dos campeonatos daquele ano se encerrarem.
Ou seja, não faria sentido nenhum esperar o ano acabar para ter acesso aos resultados financeiros e então prever a pontuação de um time.
Pois, nesse momento, todos já saberiam a pontuação real do clube.
Portanto, iremos usar as variáveis financeiras do ano anterior para prever as classificações de cada time.
Importando os dados
Os dados estão disponíveis aqui.
Foram utilizados os dados referentes aos anos entre 2014 e 2018.
library(readr)
library(knitr)
dados_futebol <- read_delim("dados_futebol.txt",
"\t", escape_double = FALSE, col_types = cols(Pontos = col_double()),
trim_ws = TRUE)
kable(tail(dados_futebol))| TIME | VALOR | VARIÁVEL | ANO | RANKING | Pontos |
|---|---|---|---|---|---|
| América Mineiro | 2.93 | LIQUIDEZ GERAL | 2016 | 22 | 28 |
| América Mineiro | 0.52 | END. FINANCEIRO | 2016 | 22 | 28 |
| América Mineiro | 0.34 | DEP. FINANCEIRA | 2016 | 22 | 28 |
| América Mineiro | 0.05 | COMP. ENDIVIDAMENTO | 2016 | 22 | 28 |
| América Mineiro | 0.31 | ROA | 2016 | 22 | 28 |
| América Mineiro | -0.07 | ROE | 2016 | 22 | 28 |
Buscar os dados do ano passado
Para cada pontuação, precisamos buscar os valores das variáveis financeiras correspondentes ao ano anterior.
Isto é, vamos supor que uma determinada linha da nossa tabela dados_futebol contenha as informações referentes ao Palmeiras em 2016.
Então, nos interessa saber a pontuação do Palmeiras em 2016 e as variáveis financeiras do Palmeiras em 2015.
Pois, como falei anteriormente, vamos utilizar as informações financeiras do ano anterior para prever a pontuação do clube.
A princípio, isso pode parecer difícil de calcular. Porém é muito fácil fazer essa correspondência no R.
Existem duas funções específicas para isso: lag e lead.
Usamos a função lag para buscar uma correspondência passada (nosso caso).
Já a função lead nos seria útil caso nosso interesse fosse buscar os dados do ano seguinte.
É necessário que você ordene os dados, assim criamos uma ordem lógica entre os acontecimentos.
library(dplyr)
dados_futebol_lag <- dados_futebol %>%
arrange(ANO) %>% #ordenamos os dados pelo ANO
group_by(TIME,VARIÁVEL) %>% #separamos os registros por Time e Variável Financeira
mutate(lag_valor = lag(VALOR)) #criamos uma nova coluna para o valor da
#variável financeira do último ano.
kable(tail(dados_futebol_lag))| TIME | VALOR | VARIÁVEL | ANO | RANKING | Pontos | lag_valor |
|---|---|---|---|---|---|---|
| Vitória | 0.77 | LIQUIDEZ GERAL | 2018 | 17 | 37 | 0.81 |
| Vitória | 4.31 | END. FINANCEIRO | 2018 | 17 | 37 | 5.35 |
| Vitória | 1.30 | DEP. FINANCEIRA | 2018 | 17 | 37 | 1.23 |
| Vitória | 0.33 | COMP. ENDIVIDAMENTO | 2018 | 17 | 37 | 0.23 |
| Vitória | 2.93 | ROA | 2018 | 17 | 37 | 3.09 |
| Vitória | -0.56 | ROE | 2018 | 17 | 37 | 0.94 |
Manipular o formato da tabela
O formato atual da tabela mostra uma linha para cada conjunto de variável/time/ano. Porém, a partir de agora será mais fácil caso a gente crie uma coluna para cada variável financeira.
Assim, só existirá uma linha na tabela para cada time/ano. Isso faz sentido pois queremos prever a pontuação dos times, que também é apenas UMA por time/ano.
Para realizar essa transformação, usamos a função cast, da biblioteca reshape2.
library(reshape2)
dados_futebol_lag<-dcast(dados_futebol_lag,TIME + ANO + RANKING + Pontos ~ VARIÁVEL ,value.var = "lag_valor")
kable(tail(dados_futebol_lag))| TIME | ANO | RANKING | Pontos | COMP. ENDIVIDAMENTO | DEP. FINANCEIRA | END. FINANCEIRO | LIQUIDEZ GERAL | LIQUIDEZ IMEDIATA | LIQUIDEZ SECA | ROA | ROE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 125 | Vasco da Gama | 2018 | 14 | 43 | 0.30 | 2.58 | 1.63 | 0.39 | 0.00 | 0.05 | 2.22 | 0.04 |
| 126 | Vitória | 2014 | 17 | 38 | NA | NA | NA | NA | NA | NA | NA | NA |
| 127 | Vitória | 2015 | 20 | NA | 0.71 | 0.79 | 3.66 | 1.27 | 0.04 | 0.05 | 2.10 | 0.00 |
| 128 | Vitória | 2016 | 20 | 45 | 0.68 | 0.80 | 4.00 | 1.53 | 0.37 | 0.42 | 1.79 | -0.40 |
| 129 | Vitória | 2017 | 18 | 43 | 0.14 | 0.62 | 1.62 | 1.62 | 2.40 | 2.94 | 1.28 | 0.63 |
| 130 | Vitória | 2018 | 17 | 37 | 0.23 | 1.23 | 5.35 | 0.81 | 0.04 | 0.23 | 3.09 | 0.94 |
Irei alterar o nome das variáveis, adicionando o prefixo de lag, já que se referem aos valores dos anos anteriores.
names(dados_futebol_lag)[5:12]<-paste0("lag_",names(dados_futebol_lag)[5:12])Algumas linhas não possuem todos os valores, ou porque o clube não participou da 1ª divisão do campeonato em algum ano ou porque não informou as variáveis financeiras.
Portanto, vamos excluir esses registros de nosso trabalho:
dados_futebol_lag<-dados_futebol_lag[!is.na(dados_futebol_lag$Pontos),] #retirar clubes sem pontuação
dados_futebol_lag<-dados_futebol_lag[!is.na(dados_futebol_lag$`lag_COMP. ENDIVIDAMENTO`),] #retirar clubes que não informaram os dados financeirosO Modelo de Regressão
Primeiramente, quis fazer um histograma de nossa variável resposta - a pontuação dos clubes. O objetivo era visualizar a distribuição desses dados.
hist(dados_futebol_lag$Pontos)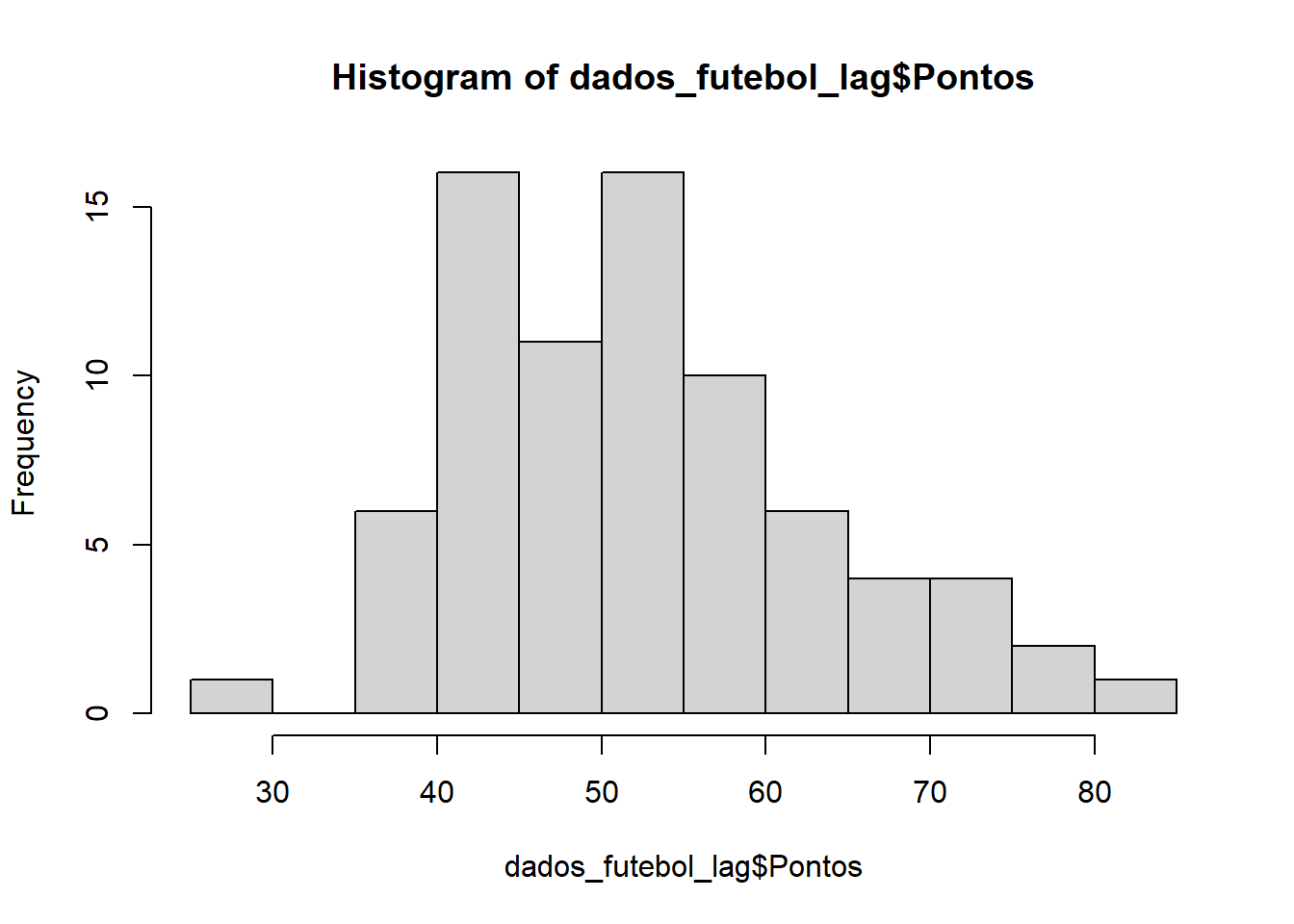
A curva da distribuição se assemelha muito a uma distribuição normal.
Para construir o modelo preditivo, iremos executar o comando a seguir.
O modelo assume que a nossa variável resposta é Pontos.
Todas as 8 variáveis financeiras do ano anterior foram definidas como variáveis preditivas.
modelo<-lm(Pontos ~ `lag_COMP. ENDIVIDAMENTO`+`lag_DEP. FINANCEIRA`+`lag_END. FINANCEIRO`+`lag_LIQUIDEZ GERAL`+`lag_LIQUIDEZ IMEDIATA`+
`lag_LIQUIDEZ SECA`+ `lag_ROA`+ `lag_ROE` ,dados_futebol_lag)
summary(modelo)##
## Call:
## lm(formula = Pontos ~ `lag_COMP. ENDIVIDAMENTO` + `lag_DEP. FINANCEIRA` +
## `lag_END. FINANCEIRO` + `lag_LIQUIDEZ GERAL` + `lag_LIQUIDEZ IMEDIATA` +
## `lag_LIQUIDEZ SECA` + lag_ROA + lag_ROE, data = dados_futebol_lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -18.587 -8.038 -1.115 5.464 29.281
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 50.50592 5.29832 9.532 4.3e-14 ***
## `lag_COMP. ENDIVIDAMENTO` 0.90657 7.23012 0.125 0.9006
## `lag_DEP. FINANCEIRA` 0.41941 1.07950 0.389 0.6989
## `lag_END. FINANCEIRO` -0.01624 0.22233 -0.073 0.9420
## `lag_LIQUIDEZ GERAL` 0.05149 2.96629 0.017 0.9862
## `lag_LIQUIDEZ IMEDIATA` -19.53367 8.14315 -2.399 0.0192 *
## `lag_LIQUIDEZ SECA` 10.47069 6.62509 1.580 0.1187
## lag_ROA -0.38105 0.62598 -0.609 0.5448
## lag_ROE 4.20419 1.91896 2.191 0.0319 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10.64 on 67 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.159, Adjusted R-squared: 0.05863
## F-statistic: 1.584 on 8 and 67 DF, p-value: 0.1463O resultado do modelo criado é que existem variáveis significativas para prever a pontuação dos clubes. Porém, o modelo não apresentou bons resultados de forma geral.
O p-value acima de 0,05 indica que o modelo não é significativo.
Em uma nova tentativa, rodei um novo modelo com apenas 3 variáveis. As três variáveis que foram mais importantes no modelo anterior.
modelo<-lm(Pontos ~ `lag_LIQUIDEZ IMEDIATA`+ `lag_LIQUIDEZ SECA`+ `lag_ROE` ,dados_futebol_lag)
summary(modelo)##
## Call:
## lm(formula = Pontos ~ `lag_LIQUIDEZ IMEDIATA` + `lag_LIQUIDEZ SECA` +
## lag_ROE, data = dados_futebol_lag)
##
## Residuals:
## Min 1Q Median 3Q Max
## -19.630 -8.026 -1.051 6.307 28.368
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 51.245 1.813 28.272 <2e-16 ***
## `lag_LIQUIDEZ IMEDIATA` -17.998 7.490 -2.403 0.0188 *
## `lag_LIQUIDEZ SECA` 8.806 5.942 1.482 0.1427
## lag_ROE 4.340 1.833 2.368 0.0206 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 10.31 on 72 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.1523, Adjusted R-squared: 0.117
## F-statistic: 4.312 on 3 and 72 DF, p-value: 0.00746O novo modelo apresentou p-value igual a 0,00746 (menor que 0,05). Isso indica que o modelo de regressão tem significância estatística para prever as pontuações dos times de futebol.
Ainda sobre o nosso modelo criado:
Uma das suposições para a aplicação da regressão linear é que os erros do modelo tenham distribuição normal. Então, podemos fazer esse teste da seguinte forma:
modelo_summary <- summary(modelo)
shapiro.test(modelo_summary$residuals) # testa se os resíduos tem distribuição normal##
## Shapiro-Wilk normality test
##
## data: modelo_summary$residuals
## W = 0.97537, p-value = 0.1456Como o p-valor é superior a 0,05 não podemos rejeitar a hipótese nula do teste, que é a normalidade dos dados.
Portanto, assumimos que os resíduos têm distribuição normal. Ou seja, a suposição é atendida para a aplicação do modelo.