Carregando as imagens e suas classificações

Carregando o nosso conjunto de dados para o objeto fashion_mnist:

fashion_mnist <- keras::dataset_fashion_mnist()

Para cada imagem do conjunto de dados, existe uma classificação. Essa classificação é um valor de 0 a 9 e representa um item de vestuário.

Para facilitar a nossa visualização, iremos adicionar os nomes de cada item!

class_names = c('Blusa',
                'Calça',
                'Pullover',
                'Vestido',
                'Casaco', 
                'Sandália',
                'Camisa',
                'Tênis',
                'Bolsa',
                'Bota de salto')

O nosso conjunto de dados possui 70.000 imagens de itens de vestuário. Desses 70 mil, 60 mil estão separados para treinarmos o nosso modelo.

Os 10 mil restantes serão utilizados para testarmos o modelo construído.

Então, precisamos guardar em objetos separados os dados de TREINAMENTO E TESTE.

train_images <- fashion_mnist$train[[1]]
train_labels <- fashion_mnist$train[[2]]
test_images <- fashion_mnist$test[[1]]
test_labels <- fashion_mnist$test[[2]]

Explorando os dados

Explorando os conjuntos de dados acima:

dim(train_images) #quantidade de imagens para o treino

## [1] 60000    28    28

dim(train_labels) #quantidade de classificações de cada imagem para o treino

## [1] 60000

dim(test_images) #quantidade de imagens para teste

## [1] 10000    28    28

dim(test_labels) #quantidade de classificações de cada imagem para teste

## [1] 10000

Então confirmamos que existem 60 mil imagens para o conjunto de treino e 10 mil imagens para o conjunto de teste. Além disso, cada imagem está representada por 28 x 28 pixels.

Veja uma imagem de forma isolada:

library(tidyr)
library(ggplot2)

image_1 <- as.data.frame(train_images[2, , ])
colnames(image_1) <- seq_len(ncol(image_1))
image_1$y <- seq_len(nrow(image_1))
image_1 <- gather(image_1, "x", "value", -y)
image_1$x <- as.integer(image_1$x)

ggplot(image_1, aes(x = x, y = y, fill = value)) +
  geom_tile() +
  scale_fill_gradient(low = "white", high = "black", na.value = NA) +
  scale_y_reverse() +
  theme_minimal() +
  theme(panel.grid = element_blank())   +
  theme(aspect.ratio = 1) +
  xlab("") +
  ylab("")

Portanto, vemos que a blusa representada na imagem acima tem uma qualidade de 28 x 28 pixels.

Então, podemos imaginar que é um gráfico, onde cada eixo (x ou y) tem 28 unidades. Cada combinação entre o eixo X e Y recebe um valor entre 0 e 255.

Caso o valor seja 0, o ponto será branco.

Caso o valor seja 255, o ponto será preto.

Entre esses extremos teremos vários tons de cinza, que ficarão mais escuros a medida que o valor se aproxima de 255.

Portanto, repare que a imagem que está sendo visualizada (uma blusa) pode ser transformada em uma matriz com 28 linhas e 28 colunas e cada elemento dessa matriz é representado por um valor entre 0 e 255.

Para criar o nosso modelo, iremos transformar a escala inicial de 0 a 255 para uma escala entre 0 e 1.

Essa transformação será feita dividindo todos os valores pelo valor máximo (255):

#colocar os valores em uma escala entre 0 e 1.
train_images <- train_images / 255
test_images <- test_images / 255

Antes de criar o nosso modelo, veja as 25 primeiras imagens do nosso conjunto de dados de treino:

#Mostrar os primeiros 25 resultados
par(mfcol=c(5,5))
par(mar=c(0, 0, 1.5, 0), xaxs='i', yaxs='i')
for (i in 1:25) { 
  img <- train_images[i, , ]
  img <- t(apply(img, 2, rev)) 
  image(1:28, 1:28, img, col = gray((0:255)/255), xaxt = 'n', yaxt = 'n',
        main = paste(class_names[train_labels[i] + 1]))
}

Criando o nosso modelo de previsão

Agora o nosso modelo irá aprender o que é uma blusa, o que é uma calça, o que é uma bolsa…

O modelo irá aprender isso tudo porque iremos mostrar 60 mil itens para ele e falar o que é cada um dos itens.

O nosso modelo terá 3 camadas:

• A primeira camada irá transformar a nossa matriz 28x28 em um vetor.
• A segunda camada irá criar 128 neurônios para a nossa rede neural
• A terceira camada irá calcular, para cada imagem, as probabilidades da imagem pertencer a qualquer uma das 10 categorias possíveis. Ou seja, a probabilidade da 1ª imagem ser uma bota, uma blusa, um vestido, etc.

model <- keras_model_sequential()
model %>%
  layer_flatten(input_shape = c(28, 28)) %>%
  layer_dense(units = 128, activation = 'relu') %>%
  layer_dense(units = 10, activation = 'softmax')

O próximo passo é compilar o modelo:

model %>% compile(
  optimizer = 'adam', 
  loss = 'sparse_categorical_crossentropy',
  metrics = c('accuracy')
)

• A função de perda mede a acurácia do modelo. Nosso objetivo é minimizar o valor dessa função.

• O função de otimização define como o modelo será atualizado de acordo com os dados e a função de perda.

• A métrica que vamos usar para monitorar o nosso modelo é a sua acurácia.

Treinando o modelo

Iremos treinar o modelo usando as 60 mil imagens de teste e as categorias correspondentes a cada imagem.

Iremos revisitar os nossos dados apenas 5 vezes.

model %>% fit(train_images, train_labels, epochs = 5, verbose = 2)

Acurácia do modelo

score <- model %>% evaluate(test_images, test_labels, verbose = 0)
cat('Perda do conjunto de TESTE:', score["loss"], "\n")

## Perda do conjunto de TESTE: 0.354217

cat('Acurácia do conjunto de TESTE:', score["accuracy"], "\n")

## Acurácia do conjunto de TESTE: 0.8726

Fazendo as nossas predições

Para fazer as predições, basta aplicar o nosso modelo nas imagens que separamos para a fase de teste do modelo:

predictions <- model %>% predict(test_images)

Pronto, as previsões das categorias das 10 mil imagens do conjunto de teste estão salvas no objeto predictions.

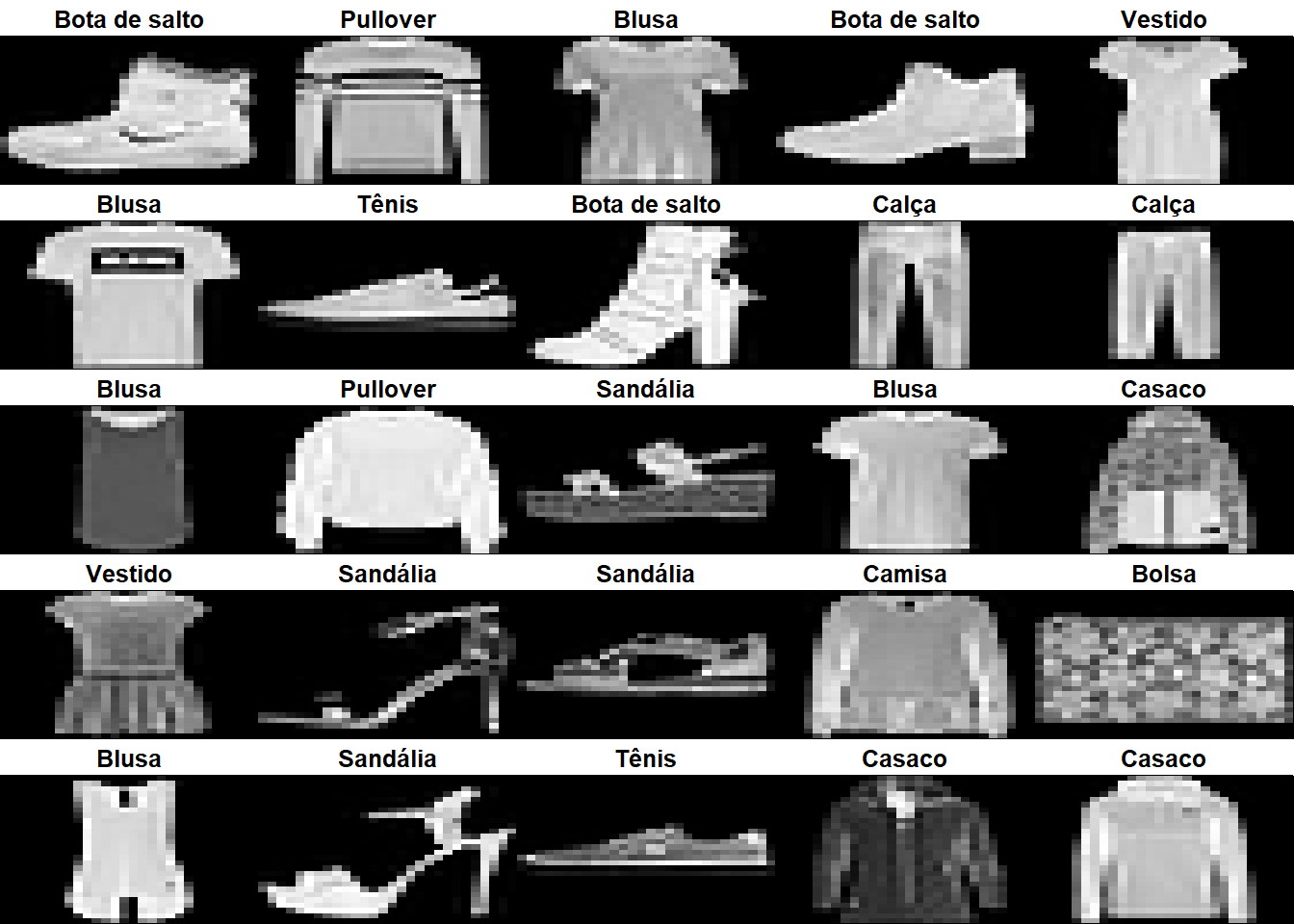
Visualização das previsões

Com o modelo já finalizado, podemos visualizar alguns resultados:

par(mfcol=c(5,5))
par(mar=c(0, 0, 1.5, 0), xaxs='i', yaxs='i')
for (i in 1:25) { 
  img <- test_images[i, , ]
  img <- t(apply(img, 2, rev)) 
  # subtract 1 as labels go from 0 to 9
  predicted_label <- which.max(predictions[i, ]) - 1
  true_label <- test_labels[i]
  if (predicted_label == true_label) {
    color <- '#008800' 
  } else {
    color <- '#bb0000'
  }
  image(1:28, 1:28, img, col = gray((0:255)/255), xaxt = 'n', yaxt = 'n',
        main = paste0(class_names[predicted_label + 1], " (",
                      class_names[true_label + 1], ")"),
        col.main = color)
}